The generic equation for the surface area of a cylinder is .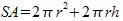
Since multi-variable equations aren't of much use here, h can be rewritten in terms of r as 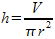. This yields an equation of .
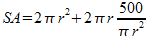This equation is then graphed in order to find the point where surface area is the smallest, with X being radius and Y being surface area.

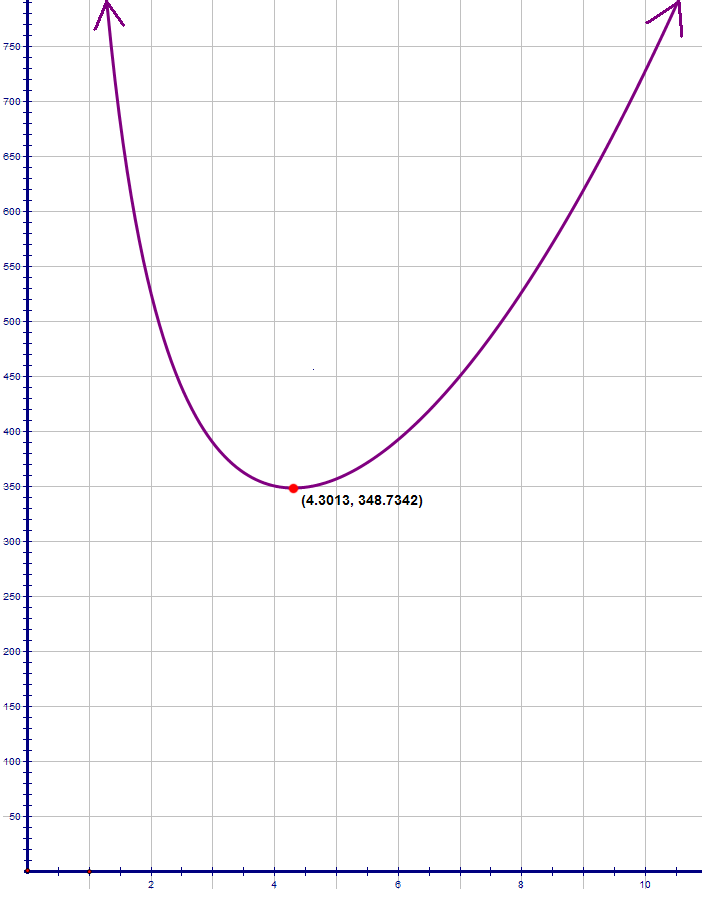
Using the calc-minimum function of the TI-83/84, the vertex is found to be approximately

(4.3013, 348.7342)

. Thus, the radius is plugged back into the equation for height to find that the corresponding height is

8.6025 cm

.
Therefore, the ratio of the radius to the height is .
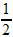